単純ランダムウォークに関する逆正弦法則
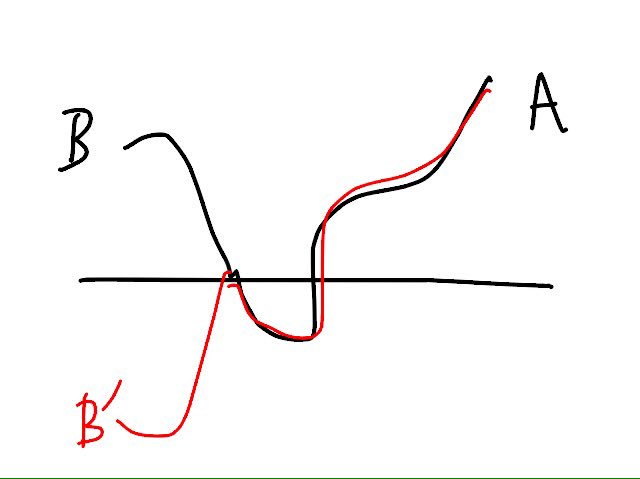
#数楽 BからAへの経路で直線と共通点を持つものの方で考える。Bから直線と最初にぶつかるところまでの部分を直線について線対称変換するとB'からAへの経路が得られる。逆対応の構成も同様。同じ方法がカタラン数の話でも出て来る。pic.twitter.com/KSiZzdUd62
#数楽 https://twitter.com/mathedr/status/792128352505122816 …一つ前のツイートはリンク先への解説のつもり。ポイントは「AからBへの経路で直線と共通点を持つものとAからB'への経路の間に長さを保つ一対一対応があること」であり、点Cは対称点B'と違ってそのために利用できない。
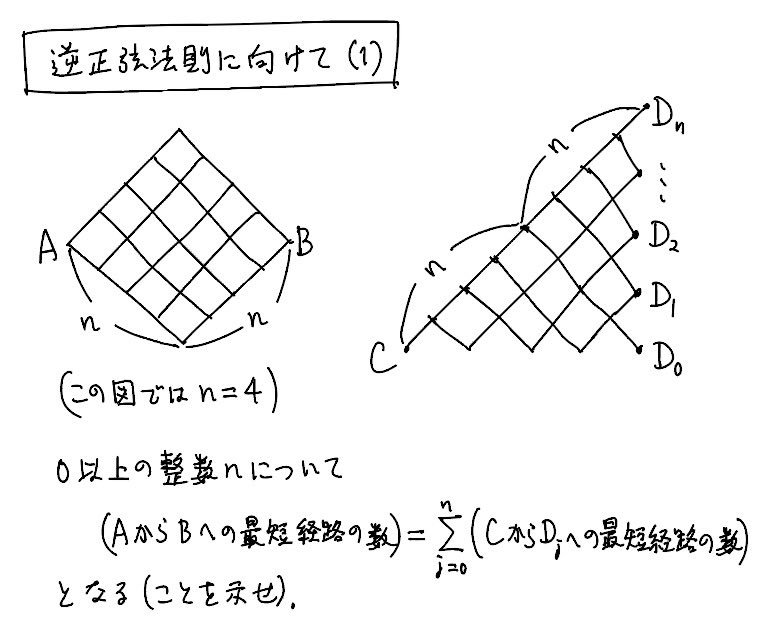
#数楽 最短経路の個数の簡単な問題(高校レベルのはず)。左図のAからBへの最短経路の個数と右図のCから左端の任意の点までの最短経路の個数が等しいことを示せ。実はこの結果は確率論における逆正弦法則の帰納法による証明の最初の段階そのもの。色々な証明法があると思う。pic.twitter.com/03Tt3QGjHS

#数楽 問題(2)。こちらの結果は逆正弦法則の証明における帰納法のステップを一つ進めるときに使われます。個人的に上の問題(1)よりもこちらの方がずっと容易だと思う。ほぼ自明に近い。pic.twitter.com/5xyTT476x5
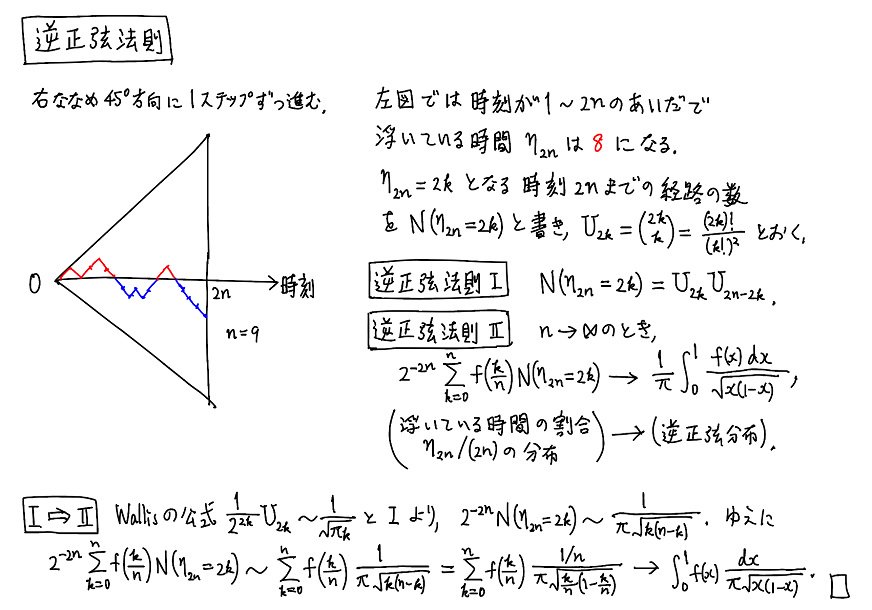
#数楽 逆正弦法則:X_jは確率1/2で±1になる独立な確率変数であるとし、W_n=X_1+…+X_nとおく。jが浮いている時刻であるとは、W_{j-1}>0またはW_j>0が成立することであると定める。u_{2n}=binom(2n,n)/2^{2n}とおく。続く
#数楽 続き。このとき、1から2nまでのうち浮いている時刻の個数が2kになる確率はu_{2k}u_{2n-2k}に等しい。この結果が逆正弦法則と呼ばれる理由は、浮いている時間の割合の確率分布がn→∞で逆正弦分布に弱収束するから。Stirlingの公式を使えば容易。
#数楽 続き。すなわち、n→∞のとき、Σ_{k=0}^n f(k/n)u_{2k}u_{2n-2k}→∫_0^1 f(x)/(π√(x(1-x))) dx確率密度函数は両端の0,1で∞に発散します。浮いている時間の割合は0や1に近くなる傾向がある。
#数楽 公平なギャンブルをやると、浮いている時間と沈んでいる時間が半分半分程度になるよりも、どちらか一方の時間の割合が長くなることの方が多い。これが逆正弦法則の意味です。
#数楽 証明はkに関する帰納法。k=0の場合は上の(1)の結果そのものであり、k-1以下の場合からkの場合を出すために(2)の公式(および(2)の公式の証明と本質的に同じ議論)を使います。(1)と(2)を自力で証明できる人にとってはそう難しくないと思います。
#数楽 (2)は経路の連結の話なのでわかってしまえば自明。問題は(1)の証明。私は代数計算をあまりせずに、お絵描きによる図形的直観に頼る証明で対処しました。まず「反射原理」を使い、図形内の最短経路は合同で保たれることを使う。代数計算よりも図形的直観に頼る証明の方がよいと思う。
#数楽 続き。上の方で出した問題は明らかに高校レベル(中学校レベルかも)です。場合の数を数えることになれていないと面倒かもしれませんが、逆正弦法則のようなちょっと面白い普遍的な数学的結果に繋がる議論なので価値は高いと思う。価値の高そうな問題を解く方が楽しいと思う。
#数楽 問題(1)や反射原理はカタラン数の「格子状の経路の数え上げ」の話と関係があります。https://ja.m.wikipedia.org/wiki/カタラン数 …https://en.m.wikipedia.org/wiki/Catalan_number … のSecond proofに反射原理の詳しい説明があります。
#数楽 高校などで、格子上の最短経路の場合の数を求める問題をやるなら、せっかくなので、カタラン数や逆正弦法則までちょっとだけ足をのばしてみる方が健全な勉強の仕方だと思う。
#数楽 一般に数学的な事柄は、ある程度先まで進んでみないと、単に複雑に見えることをやっているだけなのか、それ以上の特別な価値があることをやっているのかの判別がつかないと思う。ややこしい公式の暗記を強制され、それに従うだけなのはものすごく不健全。精神的によろしくない。
#数楽 続き。例えば高校1年でやるx^3+y^3+z^3-3xyzの因数分解の公式を暗記ですませるのは極めて精神的によろしくない。まず、1の原始3乗根ωを使えば(x+y+z)(x+ωy+ω^2z)(x+ω^2y+ωz)と完全にばらけることに触れていない。続く
#数楽 続き。教科書に載っている因数分解の公式は中途半端なせいで覚えるのが難しい。中途半端な難しい公式は暗記する価値がない。さらに、その因数分解の公式を使うと3次方程式の解の公式を作れることにも触れていない。せっかく面白い応用があるのに全然触れないのは不健全の極み。
#数楽 続き。何の価値があるのかわからない複雑な公式を暗記させられて、さらに何の価値があるのか不明の単に複雑なだけに見える問題を解くことを強制させられる。これはつらい。しかも、本当の数学はそういうつまらない分野ではない。
#数楽 高校1年で習う因数分解の公式の3次方程式の解法への応用についてはリンク先の連続ツイートを見てください。https://twitter.com/genkuroki/status/668191582005231616 …
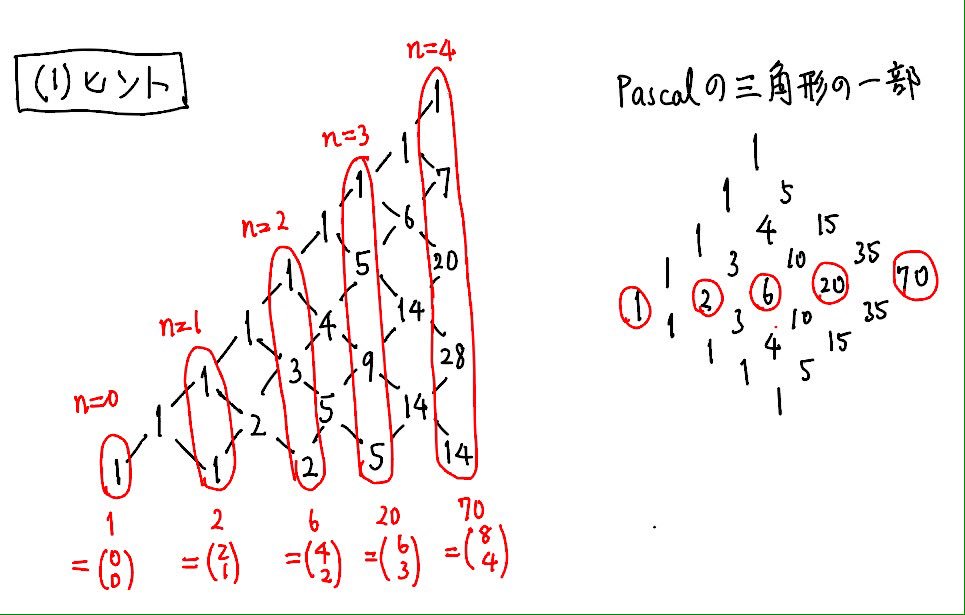
#数楽 昨晩の問題(1)https://twitter.com/genkuroki/status/793828530467381248 …のヒント。いや、「ヒント」.というより「問題が正しいことの数値的証拠」と言うべきか。私は結局、ヒント図の方法ではなく、お絵描き直観の方法で証明しました。問題を一般化した方が楽に解けると思う。pic.twitter.com/v6oZxbEYe2
#数楽 続き。ここで「お絵描き直観の方法」とは「描いた図形をそのままその図形に関するある量(今の場合は左端から右端への最短経路の数)だとみなし、図形の操作によってすべてを直観的に計算すること」です。これ、結構便利です。絵をそのまま式だと思う。
#数楽 左から右に進むときに必ず斜め45度に1ステップ進むことにする。進み方に制限が無ければ、左端から右端への経路の総数を求める問題は二項係数の和を求める単純な問題になる。問題は「これより下に行ってはいけない」のような制限がある場合。しかしその制限は「反射原理」で無害化できる。
#数楽 続き。反射原理の説明は https://twitter.com/genkuroki/status/792149425284009984 … にある。「直線の川に立ち寄る最短経路を求めよ」というタイプのよくあるパズルの解法の考え方そのものなので、「反射原理」のような言い方は大げさかも。
#数楽 単純ランダムウォークの解説についてはhttp://zakii.la.coocan.jp/enumeration/70_diffusion.htm …http://web.econ.keio.ac.jp/staff/hattori/srw.pdf …を見て下さい。後者には逆正弦法則の証明の解説もある(しかしあまり整理されていない)。前者はリンクをたどると続きを読めます。
#数楽 現時点での私の理解では、逆正弦法則の証明を理解するための最短コースはhttps://twitter.com/genkuroki/status/793828530467381248 … を解く↓https://twitter.com/genkuroki/status/793834575671681025 … も解く↓http://web.econ.keio.ac.jp/staff/hattori/srw.pdf … の定理10の証明をすぐに読む
#数楽(1) https://twitter.com/genkuroki/status/793828530467381248 …(2) https://twitter.com/genkuroki/status/793834575671681025 …を解けた人用の逆正弦定理の説明(1/2)pic.twitter.com/OYCPYxGKrf

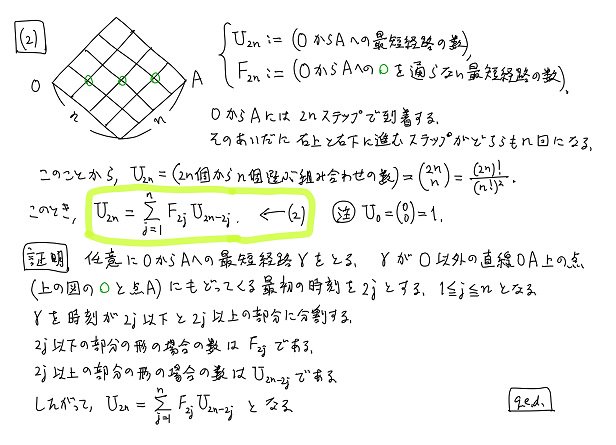
#数楽 再投稿。(2)解答。経路は初めてゼロラインに戻った前後に分割して、前の部分の形の数と後の部分の形の数の積の和で経路全体の個数を数えることができる。pic.twitter.com/6h6VjgTPSP
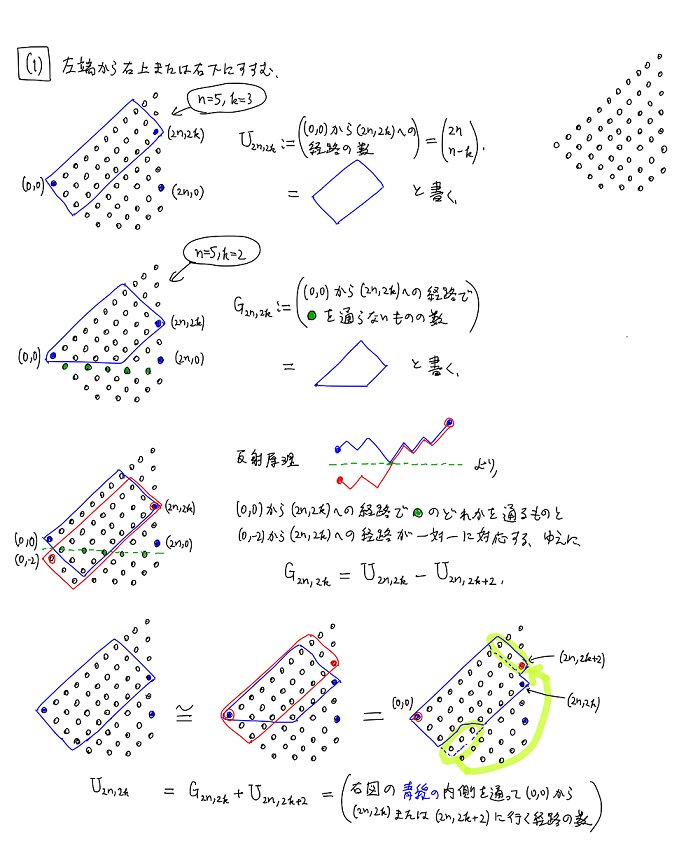
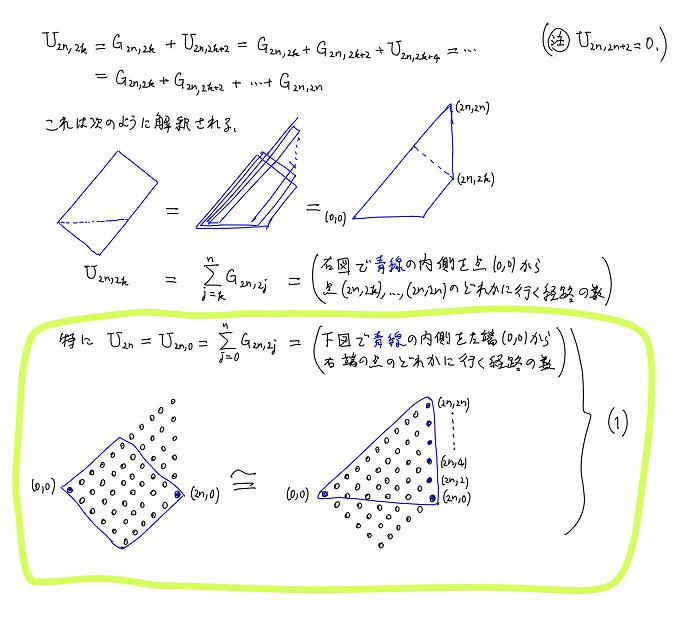
#数楽 続き。G_{2n,2k}=((2k+1)/(n+k+1))binom(2n,n-k)であり、特にG_{2n,0}=(1/(n+1))binom(2n,n)は所謂カタラン数です。G_{2n,2k}はカタラン数の一般化。
#数楽 続き。以上の単純ランダムウォークでは二項係数やカタラン数の一般化が自然に出て来たが、そのような代数的詳細によらない「お絵描き証明」になっていると良いことが結構ある。例えば二項係数やカタラン数の一般化を使ってしまうと単純でないランダムウォークに拡張できなくなる。
#数楽 正直な話、手描きの図が必要な説明をしなければいけないとき、図をパソコンなどで清書する気にはまったくなれない。手描きですませたい。黒板とチョークは便利な道具。もちろん使えるものは全部使った方がよいのですが。
#数楽 A4の計算用紙を挟むバインダーを愛用しているのですが、持ち運び用、寝る場所の側、リビングの三ヶ所に置いてあります。これは安価で優れた投資なのでおすすめ。描きながら考えると、考えることの楽しさが増す。式は書くという感覚ではなく描くという感覚に近い場合の方が楽しい。
#数楽 次のノートを追加した。http://www.math.tohoku.ac.jp/~kuroki/LaTeX/#2016-11-02 …→ http://www.math.tohoku.ac.jp/~kuroki/LaTeX/20161102ArcSineLawForSimpleRandomWalks.pdf …単純ランダムウォークの逆正弦法則 (手書きのノート)次のまとめの添付画像をPDFにまとめたものhttps://twitter.com/genkuroki/status/795079149882732544 …
#数楽 続き。一般のランダムウォークだと少し面倒になるのですが、単純ランダムウォークの場合の逆正弦法則の証明は高校レベルの「最短経路の本数を求める問題」の発展形になっています。本質的に絵を描きながら経路の一対一対応を作って行くだけで証明できる。
#数楽 「x=0から出発して、コインを投げて表が出たらx軸上の位置を1増やし、裏が出たら1減らすを繰り返す」のが単純ランダムウォークで、x軸上を進み方の確率分布がこれより複雑な場合が単純ではなより一般のランダムウォーク。https://twitter.com/genkuroki/status/795453947892924422 …
#数楽 ランダムウォークの逆正弦法則(Arcsin法則)をメルセンヌツイスタ(Excel VBA)でシミュレーションして確認。 - Fallen Physicist, Rising Engineer http://app.m-cocolog.jp/t/typecast/606783/512682/86269522 …
#数楽 某ノート http://www.math.tohoku.ac.jp/~kuroki/LaTeX/20160501StirlingFormula.pdf#page80 … (p.80)ではWallisの公式と逆正弦分布の関係に触れていますが、その続きのランダムウォークの逆正弦法則の話はhttp://www.math.tohoku.ac.jp/~kuroki/LaTeX/#2016-11-02 …にあります。
#数楽 単純ランダムウォークの逆正弦法則であれば、最短経路の本数の数え上げに関する高校数学っぽい方法とWallisの公式を組み合わせれば、かなり容易にかつ直観的に理解できます。ただし、お絵描きによる試行錯誤は必須ですが。http://www.math.tohoku.ac.jp/~kuroki/LaTeX/20161102ArcSineLawForSimpleRandomWalks.pdf …
"単純ランダムウォークに関する逆正弦法則"単純ランダムウォークに関する逆正弦法則について可能な限り直観的に説明する。公平なギャンブルで浮いている時間の割合が1/2に近い場合は0または1に近い場合よりも稀である。https://twitter.com/i/moments/847098146660368384 …
#数楽 単純乱歩の逆正弦法則の証明についてはこちらのPDFに「まとめ」があります→ http://www.math.tohoku.ac.jp/~kuroki/LaTeX/20161102ArcSineLawForSimpleRandomWalks.pdf …自分で紙に描いて試行錯誤しないと理解できないと思いますが(そうでない数学の話は算数レベルでもない)、内容はWallisの公式を除けば完全に初等的。
#数楽 高々高校レベルの数学に「適当に制限を付けた格子状の道に沿った最短経路の個数」を求める問題がありますが、Wallisの公式を除けば、単純ランダムウォークの逆正弦法則の証明は経路の個数を初等的に数える手続きでしかない。しかも直観的に数えることができる。
#数楽 m≧nとする.xy平面上を原点から出発して右に1または上に1,合わせてm+n回移動する経路のうち,点(m,n)に至るものの集合をR,x,n≧yの領域を移動するものをTとする.このときR,Tの間に自然な1対1対応がある.
証明.途中x>yを通って(m,n)に至る経路の集合をSとする.Rのうち(0,1)を通るものをR',(1,0)とx=y>0のある点を通るものをRDとする.RはS,R',RDに分かれる.
Tのうち途中x>yを通って(m,n)以外の点に至るものをT',x=y>0のある点を通るものをTDとする.TはS,T',TDに分かれる.帰納法の仮定より,R'とT'の間,RDとTDの間に1対1対応がある.証明終.
RからTへの全単射は次のように得られる.非負整数kに対し,直線y=x+kを初めて超える上移動を右移動に置き換える.
#数楽 現在 http://math.tohoku.ac.jp/~kuroki/LaTeX/ にアクセスできなくなっています。最近ずっと使いまわしている解説のコピーを以下の場所に置いておきました。http://genkuroki.web.fc2.com/20160501StirlingFormula.pdf …http://genkuroki.web.fc2.com/20160616KullbackLeibler.pdf …
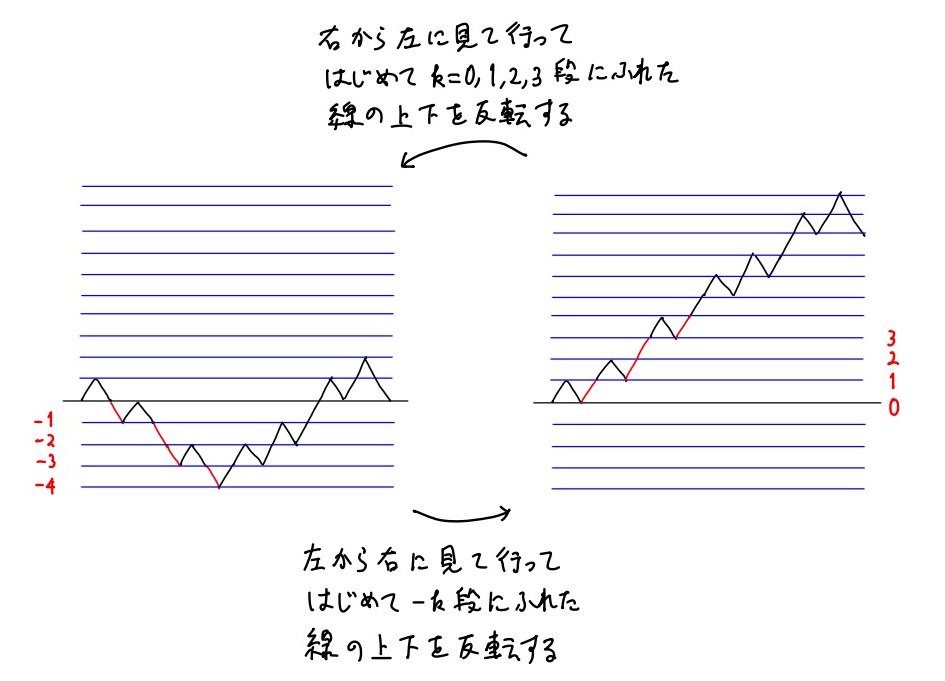
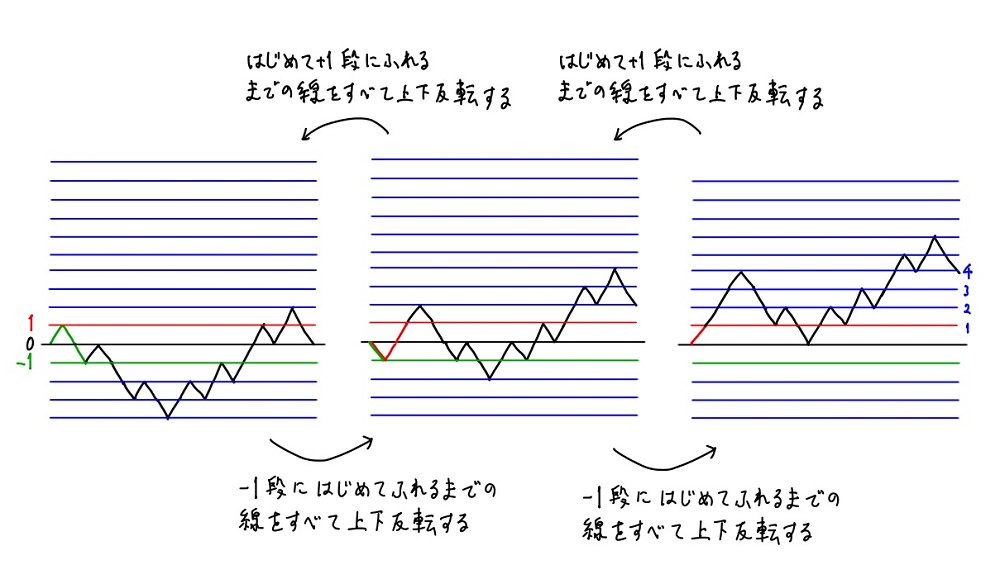
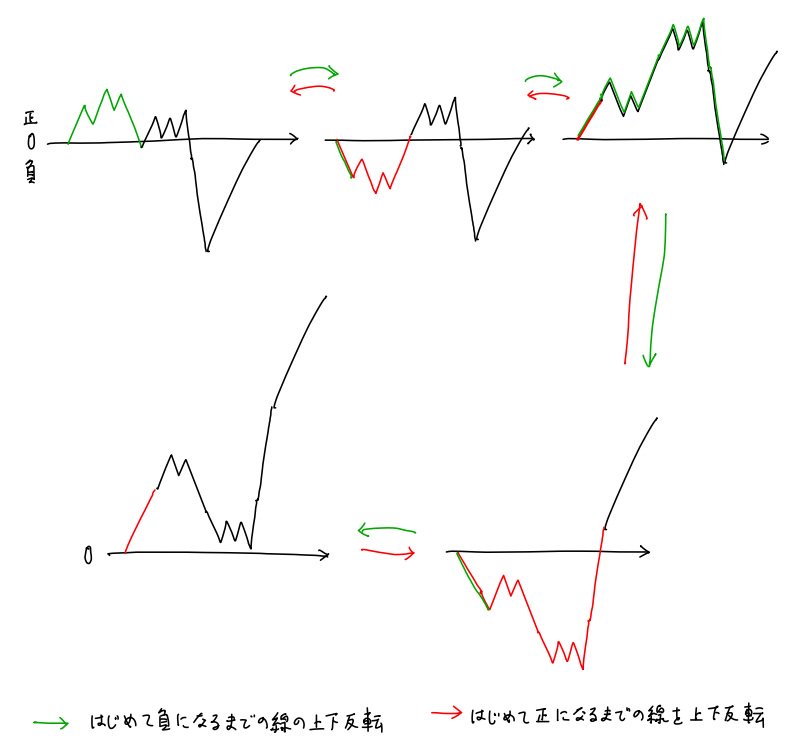
#数楽 続き。私による一対一対応の作り方は「-1段に初めて触れるまでの線の上下をすべて反転する」と「1段に初めて触れるまでの線の上下をすべて反転する」の繰り返し。反射原理を繰り返し用いている。ランダムウォークの話は様々な一対一対応が作れて面白いですね。pic.twitter.com/YK1GnZCfrg
#数楽 続き。単純とは限らない一般のランダムウォークにも適用できる経路の一対一対応に関してはリンク先のまとめを見て下さい。「等価原理」を初等的に示すことができる。https://twitter.com/i/moments/847101031146176512 …
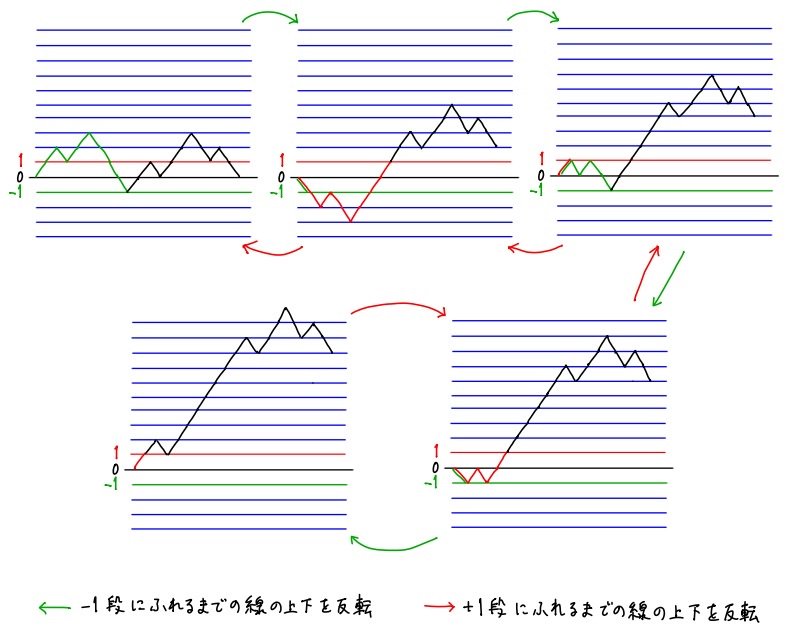
#数楽 私による一対一対応の図の例があまりにもダメだったので一対一対応の作り方を説明するための別の図を投稿。pic.twitter.com/vRT1Hbrde9